Imagine I just lost a game of chess. You might infer that I’m disappointed or not very good at chess. Without any additional information, you probably wouldn’t infer that I wanted to lose the game. Yet, that is the inference that most inverse reinforcement learning (IRL) methods would make. Nearly all of them assume, incorrectly, that the human is (approximately) rational.
Unsurprisingly, an inaccurate model of the human can lead to perverse inferences; many have constructed and pointed out examples of such (Steinhardt and Evans, 2017; Evans, 2016; Shah, 2019). Here, however, I’m going to talk about a seemingly contradictory phenomenon, one that was originally quite perplexing to us: a better human model can lead to worse reward inference. The reason is that we usually evaluate human models in terms of prediction. However, a more predictive human model does not necessarily imply better inference.
Case study: better human model, but worse reward inference?
One setting where the standard assumption fails is in collaborative environments where the human is aware that the system (“robot”) needs to learn from their demonstrations. In collaborative settings, humans may act pedagogically and to try to teach the robot the reward function. However, optimizing for teaching the reward function is different from optimizing for the reward function itself (the standard assumption).
Intuitively, using a more accurate model of the human should result in better reward inference. Thus, we would expect that when the human is pedagogic, the robot can improve its inference by explicitly modeling the human as pedagogic. In theory, this is certainly true, and indeed it is the direction suggested and pursued by prior work (Fisac, 2018; Malik, 2018). However, as part of our upcoming UAI 2019 paper, we tested this in practice, and found it to be much more nuanced than expected.
Experimental setup
We tested the impact of modeling pedagogy on reward inference by performing additional analyses on human studies originally performed by Ho et al (2016). Ho et al (2016) conducted an experiment to test whether humans do indeed pick more informative demonstrations in pedagogic settings. In their study, participants were split into two conditions, which I’ll refer to as the literal and the pedagogic condition. Participants in the literal group tried to maximize the reward of their demonstration, while participants in the pedagogic group tried to teach the reward to a partner who would see their demonstration. The environments they tested were gridworlds that were made up of three differently colored tiles. Each color could either be safe or dangerous, leading to eight possible reward functions.
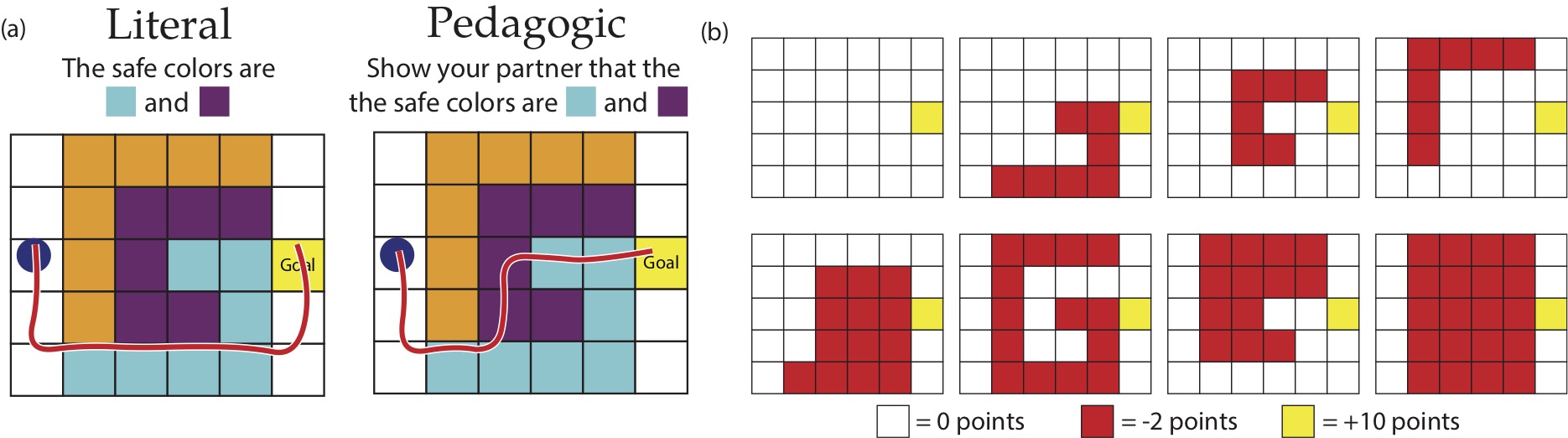(a) The instructions given to participants in the literal and pedagogic condition, and a sample demonstration from both conditions. (b) All possible reward functions. Each tile color can be either safe (0 points) or dangerous (-2 points). Figure modified from Ho et al (2018).
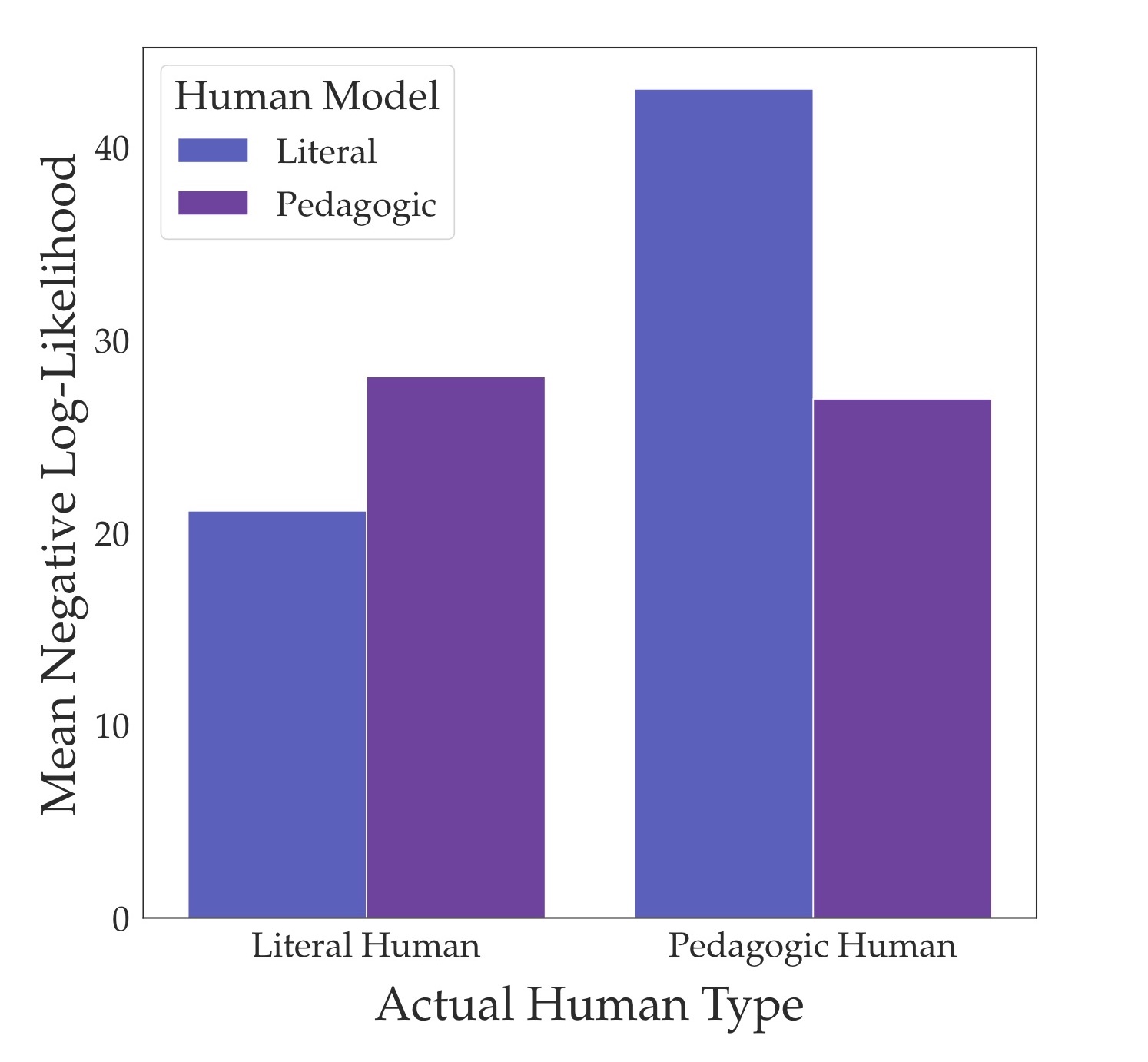
Participants in the pedagogic condition did indeed choose more communicative demonstrations. For example, they were more likely to visit all safe colors and to loop over safe tiles multiple times. To quantitatively model the difference between the humans in both conditions, Ho et al (2016, 2018) developed what I’ll call the literal model and the pedagogic model. The literal model is the standard model – the human optimizes for the reward function directly. The pedagogic model, on the other hand, assumes that the human optimizes for teaching the reward function. Compared to the literal model, they found that the pedagogic model was a much better fit to humans in the pedagogic condition. In the figure below, we plotted the log-likelihood of demonstrations under both models for both conditions:
Improving the robot’s inference?
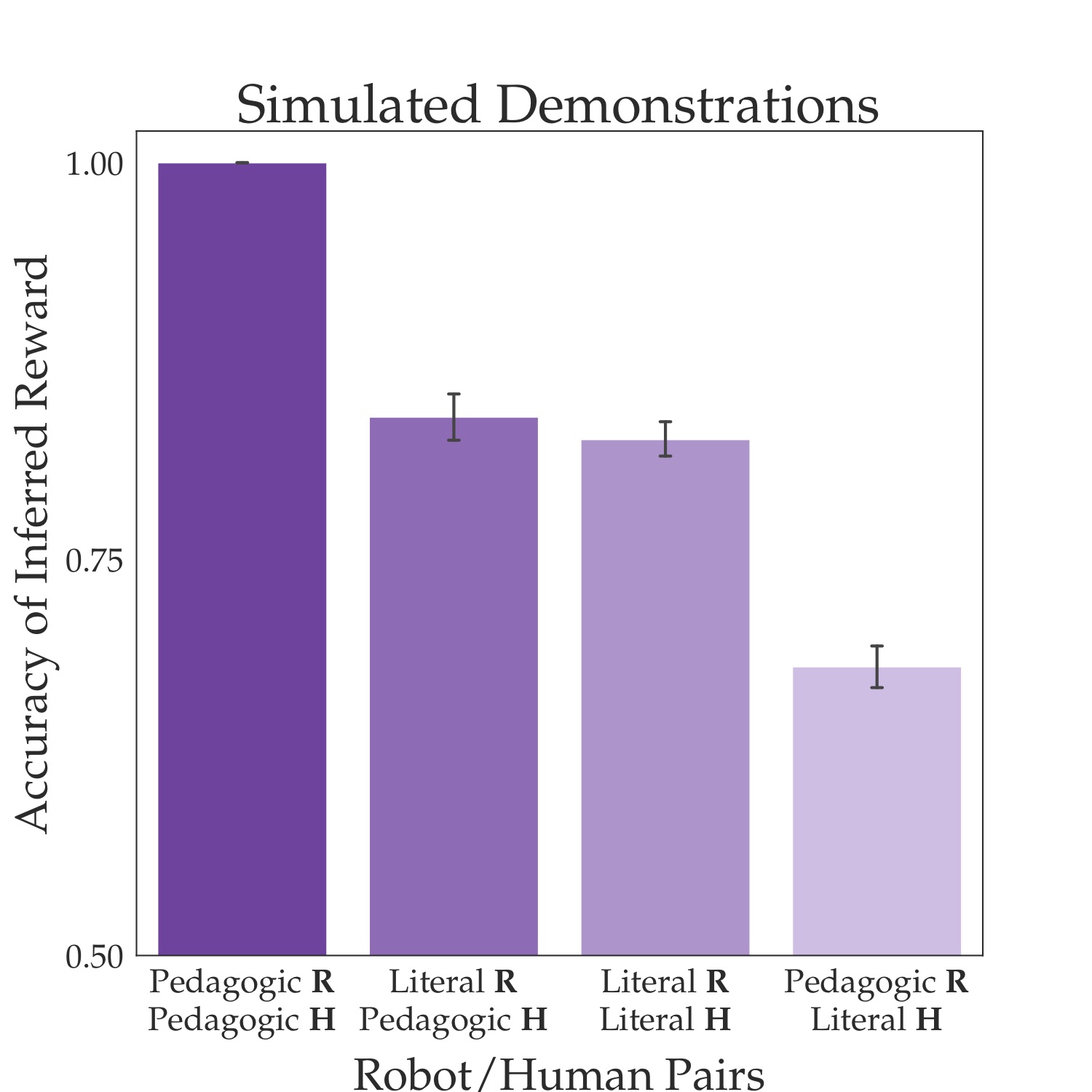
Turning to the robot side, we analyzed whether the robot’s inference could benefit from explicitly modeling the human as pedagogic. We tested a literal robot, which uses the literal model of the human, and a pedagogic (often referred to as “pragmatic”) robot, which uses the pedagogic model of the human. If we test these two robots with humans simulated according to the literal and pedagogic human model, then we get exactly what we would expect. When the human is pedagogic, the robot has a higher accuracy of reward inference if it models the human as being pedagogic (first bar from left) than if it models the human as being literal (second bar), and the advantage is quite large:
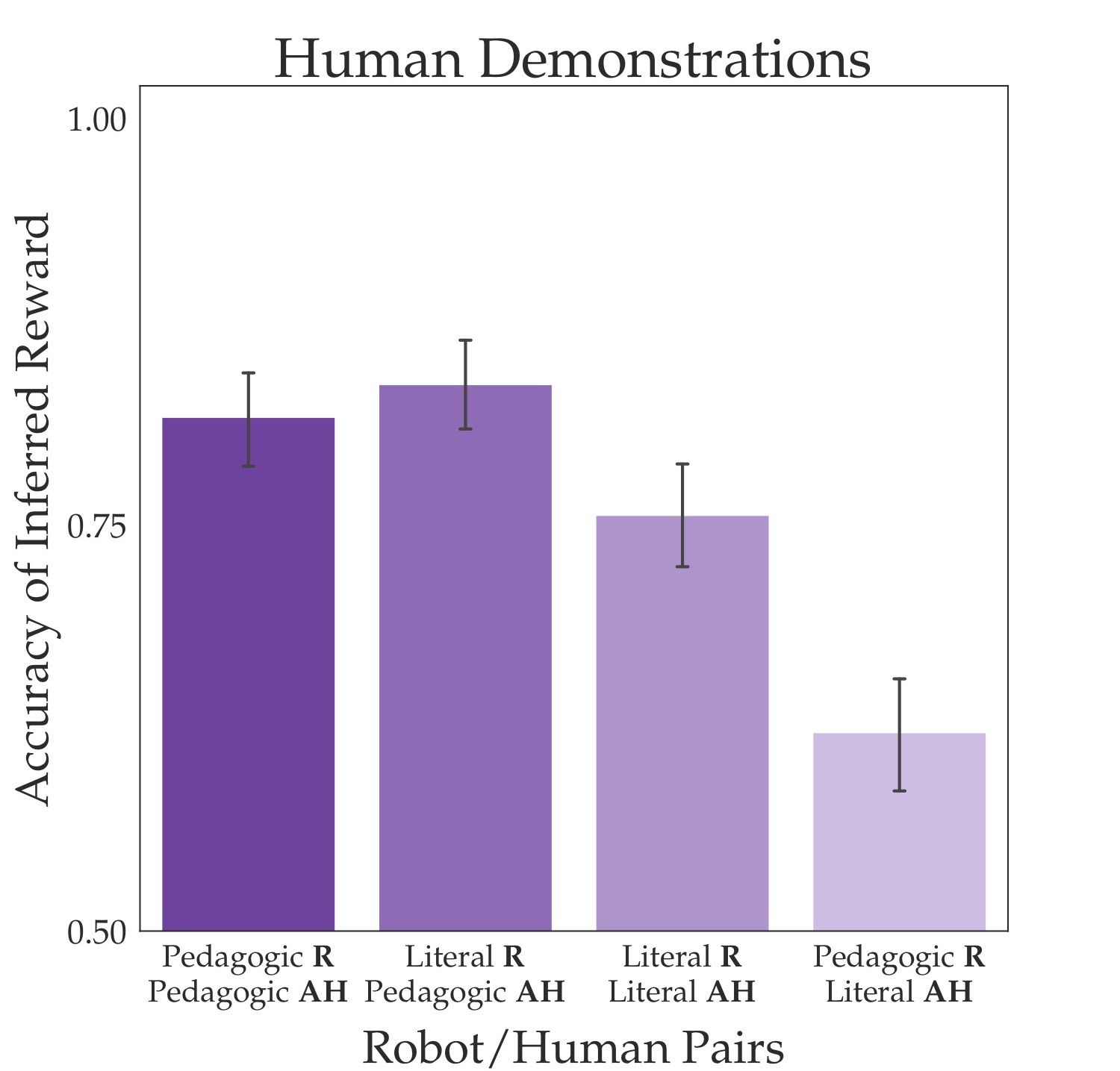
But, if we test the two models with actual humans (abbreviated AH), then we get puzzling results. The large advantage that the pedagogic robot had disappears. When the human is pedagogic, the pedagogic robot now does no better than the literal robot, and in fact it does slightly worse. What’s the deal?
An explanation: forward versus reverse model
Why does using the pedagogic model not improve reward inference? My first reaction was that the pedagogic model was “wrong”. But then I plotted the log-likelihoods under the pedagogic and literal model (see figure above) and verified that the pedagogic model is a much better fit than the literal model to the humans from the pedagogic condition. So simply saying that the pedagogic model is misspecified is too crude of an answer. Because in that case the literal model is “more” misspecified, so why doesn’t it do worse?
It’s not about generalization either. We’re testing reward inference in the exact same population that the literal and pedagogical models were fit to. So surely, at least in this idealized example, the pedagogic model should improve reward inference.
Finally, I realized why the results felt paradoxical. I assumed the pedagogic model was “better” because it was a “better fit” to human behavior because it was better at predicting human demonstrations. However, just because a model is better for prediction does not mean that it is better for inference. In other words, even if a model is better at predicting human behavior, it is not necessarily a better model for the robot to use to infer the reward.
Another way to see it is that the best forward model is not the same as the best reverse model. When we talk about a “human model”, we typically mean a forward model for the human, a model that goes from reward to behavior. To perform reward inference, we need a reverse model, a model that goes from behavior to reward. For the sake of inference, it is common to convert a forward model into a reverse model. For example, through Bayes’ rule, which is what we do in the pedagogy case study. But, crucially, the ranking of models is not guaranteed to be preserved after applying Bayes’ rule (or a more general conversion method). That is, suppose we have forward models A and B such that A is better than B (in terms of prediction). Once they are converted into reverse models A’ and B’, it may be the case that B’ is better than A’ (in terms of inference).
I think the reason our results felt paradoxical is that we have an intuition that inversion, i.e. applying Bayes’ rule, should preserve the ranking of models, but this is just not the case. (And no, it’s not about the prior being misspecified. In our controlled experiment, there is a ground-truth prior, the uniform distribution.) Maybe it doesn’t feel counterintuitive to you, but if it does, see the toy example in the next section.
Prediction vs inference: a toy example
Suppose there is a latent variable \(\theta \in \Theta\) with prior distribution \(p(\theta)\) and observed data \(x \in \mathcal{X}\) generated by some distribution \(p(x \mid \theta)\). In our setting, \(\theta\) corresponds to the reward parameters and \(x\) corresponds to the human behavior. For simplicity, we assume \(\Theta\) and \(\mathcal{X}\) are finite. We have access to a training dataset \(\mathcal{D} = \{(\theta_i, x_i)\}_{i=1}^n\) of size \(n\). A predictive model \(m(x \mid \theta)\) models the conditional probability of the data \(x\) given latent variable \(\theta\) for all \(x \in \mathcal{X}, \theta \in \Theta\). In our case, the predictive model is the forward model of the human. The predictive likelihood \(\mathcal{L}_{\mathcal{X}}\) of a predictive model \(m\) is simply the likelihood of the data under the model:
\[\mathcal{L}_{\mathcal{X}}(m) = \prod_{i=1}^n m(x_i \mid \theta_i)\,.\]The inferential likelihood is the likelihood of the latent variables after applying Bayes’ rule:
\[\mathcal{L}_{\Theta}(m) = \prod_{i=1}^{n} \frac{m(x_i \mid \theta_i)p(\theta_i)}{\sum_{\theta}m(x_i \mid \theta)p(\theta)} \,.\]Predictive likelihood does not necessarily imply higher inferential likelihood. In particular, there exist settings in which there are two predictive models \(m_1, m_2\) such that \(\mathcal{L}_{\mathcal{X}}(m_1) > \mathcal{L}_{\mathcal{X}}(m_2)\), but \(\mathcal{L}_{\Theta}(m_1) < \mathcal{L}_{\Theta}(m_2)\).
For example, suppose that \(\Theta = \{\theta_1, \theta_2\}\) and \(\mathcal{X} = \{x_1, x_2, x_3\}\), the prior \(p(\theta)\) is uniform over \(\Theta\), and the dataset \(\mathcal{D}\) contains the following \(n=9\) items: \(\mathcal{D} = \{(\theta_1, x_1), (\theta_1, x_1), (\theta_1, x_2), (\theta_2, x_2), (\theta_2, x_2), (\theta_2, x_3), (\theta_2, x_3), (\theta_2, x_3), (\theta_2, x_3)\}\)
Define the models \(m_1(x \mid \theta)\) and \(m_2(x \mid \theta)\) by the following conditional probabilities tables.
| $$x_1$$ | $$x_2$$ | $$x_3$$ | |
| $$\theta_1$$ | $$2/3$$ | $$1/3$$ | $$0$$ |
| $$\theta_2$$ | $$0$$ | $$1/3$$ | $$2/3$$ |
| $$x_1$$ | $$x_2$$ | $$x_3$$ | |
| $$\theta_1$$ | $$2/3$$ | $$1/3$$ | $$0$$ |
| $$\theta_2$$ | $$0$$ | $$2/3$$ | $$1/3$$ |
The model \(m_1\) has predictive likelihood \(\mathcal{L}_{\mathcal{X}}(m_1) = (2/3)^6(1/3)^3\) and inferential likelihood \(\mathcal{L}_{\Theta}(m_1) = (1/2)^3\). The model \(m_2\) has predictive likelihood \(\mathcal{L}_{\mathcal{X}}(m_2) = (2/3)^4(1/3)^5\) and inferential likelihood \(\mathcal{L}_{\Theta}(m_2) = (1/3)(2/3)^3\). Thus, \(\mathcal{L}_{\mathcal{X}}(m_1) > \mathcal{L}_{\mathcal{X}}(m_2)\), but \(\mathcal{L}_{\Theta}(m_1) < \mathcal{L}_{\Theta}(m_2)\).
The key reason for the discrepancy is that predictive likelihood normalizes over the space of observations \(\mathcal{X}\), while inferential likelihood normalizes over the space of latent variables \(\Theta\). It may seem surprising that the normalization can have such an impact. But the difference is precisely what creates the difference between optimizing for prediction and optimizing for inference and is what leads to e.g. the difference between predictive robot motion and legible robot motion (Dragan et al, 2013).
Conclusion
My claim that a better human model can lead to worse reward inference was, admittedly, underspecified. As we’ve seen, it depends on how you define “better” – in terms of prediction or inference. But I left it underspecified for a reason. I believe most people automatically fill in “better” with “more predictive”, and I wanted to demonstrate how that inclination can lead us astray. While I believe better prediction probably does usually lead to better inference, as illustrated by this example, it is not a logical necessity, and we should be wary of that.
For details on everything in this post, as well other points about misspecification in reward learning, you can check out our paper.
Thanks to Jacob Steinhardt, Frances Ding, and Andreas Stuhlmüller for comments on this post.
References
Dragan, A. D., Lee, K. C., & Srinivasa, S. S. “Legibility and predictability of robot motion.” HRI 2013.
Evans, O., Stuhlmüller, A., and Goodman N. “Learning the preferences of ignorant, inconsistent agents.” AAAI 2016.
Fisac, J., Gates, M. A., Hamrick, J. B., Liu, C., Hadfield-Menell, D., Palaniappan, M., Malik, D., Sastry S. S., Griffiths T. L., and Dragan A. D. “Pragmatic-pedagogic value alignment.” ISRR 2018.
Ho, M. K., Littman, M., MacGlashan, J., Cushman, F. and Austerweil, J. L. “Showing versus doing: Teaching by demonstration.” NeurIPS 2016
Ho, M. K., Littman, M. L., Cushman, F., and Austerweil, J. L. “Effectively Learning from Pedagogical Demonstrations.” CogSci 2018.
Malik, D., Palaniappan, M., Fisac, J. F., Hadfield-Menell, D., Russell, S., and Dragan, A. D. “An Efficient, Generalized Bellman Update For Cooperative Inverse Reinforcement Learning.” ICML 2018.
Milli, S., Dragan, A. D. “Literal or Pedagogic Human? Analyzing Human Model Misspecification in Objective Learning” UAI 2019.
Shah, R., Gundotra, N., Abbeel, P. and Dragan, A. D. “On the Feasibility of Learning, Rather than Assuming, Human Biases for Reward Inference.” ICML 2017.
Steinhardt, J. and Evans, O. “Model misspecification and inverse reinforcement learning.” https://jsteinhardt.wordpress.com/ 2017/02/07/model-mis-specificationand-inverse-reinforcement-learning/. 2017.